生存分析实战

一. 概述

生存分析是一种统计方法，主要用于研究某个事件（如死亡、故障、客户流失）发生前的时间长度及其影响因素。它的核心特点是能处理“删失数据”（censored data），即部分研究对象在观察期内未发生目标事件（如患者未死亡、设备未故障）。

该博客是一篇学习笔记，以下是全文框架。

  • 卡普兰-迈耶生存曲线（Kaplan-Meier）与对数秩检验（Log-Rank Test）

  • Cox比例风险模型（Cox Proportional Hazards）

  • 加速失效时间模型（Accelerated Failure Time）

  • 将生存分析模型结果可视化，方便真实模拟业务场景

以下资源在创建此博客时被参考。

https://notebooks.databricks.com/notebooks/CME/Survival_Analysis/index.html#Survival_Analysis_1.html

二. 数据读取与预处理

1. 导入相应的Python库

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# PySpark相关库
from pyspark import SparkConf
from pyspark.sql.functions import col, when
from pyspark.sql import SparkSession
from pyspark.sql.types import StructType, StructField, DoubleType, StringType, IntegerType

# 数据处理与可视化库
from matplotlib import pyplot
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

# 生存分析库
from lifelines import KaplanMeierFitter
from lifelines.utils import median_survival_times
from lifelines.statistics import pairwise_logrank_test, proportional_hazard_test
from lifelines.fitters.coxph_fitter import CoxPHFitter
from lifelines import KaplanMeierFitter, WeibullAFTFitter,LogNormalAFTFitter,LogLogisticAFTFitter

# 交互式可视化库
from ipywidgets import interact, widgets
from IPython.display import display

2. 数据导入

数据来源：https://github.com/IBM/telco-customer-churn-on-icp4d/blob/master/data/Telco-Customer-Churn.csv

数据说明：

  1. 客户信息
列名 数据类型 说明
customerID String 客户唯一标识符
gender String 性别（Male/Female）
seniorCitizen Double 是否为老年人（0=否, 1=是）
partner String 是否有配偶（Yes/No）
dependents String 是否有经济依赖人（Yes/No）
  1. 服务使用情况
列名 数据类型 说明
tenure Double 客户使用服务的月数（客户生命周期）
phoneService String 是否开通电话服务（Yes/No）
multipleLines String 是否开通多线电话（Yes/No/No phone service）
internetService String 互联网服务类型（DSL, Fiber optic, No）
onlineSecurity String 是否开通在线安全服务（Yes/No/No internet service）
onlineBackup String 是否开通在线备份服务（Yes/No/No internet service）
deviceProtection String 是否开通设备保护服务（Yes/No/No internet service）
techSupport String 是否开通技术支持服务（Yes/No/No internet service）
streamingTV String 是否开通流媒体电视（Yes/No/No internet service）
streamingMovies String 是否开通流媒体电影（Yes/No/No internet service）
  1. 合同与账单信息
列名 数据类型 说明
contract String 合同类型（Month-to-month, One year, Two year）
paperlessBilling String 是否使用无纸化账单（Yes/No）
paymentMethod String 支付方式（Electronic check, Mailed check, Bank transfer, Credit card）
monthlyCharges Double 月度费用（美元）
totalCharges Double 总费用（美元，历史累计）
  1. 目标变量（预测核心）
列名 数据类型 说明
churn String 客户是否流失（Yes/No） 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
conf = SparkConf().setAppName("Q2").set("spark.jars", "/data/lab/mysql-connector-j-8.4.0.jar")
spark = SparkSession.builder.config(conf=conf).appName("Q2").getOrCreate()

# 设定文件路径
data_path = '/data/lab/pro1/Telco-Customer-Churn.csv'

# 定义schema
schema = StructType([
  StructField('customerID', StringType()),
  StructField('gender', StringType()),
  StructField('seniorCitizen', DoubleType()),
  StructField('partner', StringType()),
  StructField('dependents', StringType()),
  StructField('tenure', DoubleType()),
  StructField('phoneService', StringType()),
  StructField('multipleLines', StringType()),
  StructField('internetService', StringType()), 
  StructField('onlineSecurity', StringType()),
  StructField('onlineBackup', StringType()),
  StructField('deviceProtection', StringType()),
  StructField('techSupport', StringType()),
  StructField('streamingTV', StringType()),
  StructField('streamingMovies', StringType()),
  StructField('contract', StringType()),
  StructField('paperlessBilling', StringType()),
  StructField('paymentMethod', StringType()),
  StructField('monthlyCharges', DoubleType()),
  StructField('totalCharges', DoubleType()),
  StructField('churn', StringType())
  ])

3. 数据预处理

1
2
3
4
5
6
7
8
9
10
# 原始文件存在bronze_df表中
bronze_df = spark.read.format('csv').schema(schema).option('header','true').load(data_path)
bronze_df.show(5)

# 进行数据预处理,将处理好的数据放在silver_df中
# 将“churn”列转换为布尔值，并过滤出有月度合同的互联网用户。
silver_df = bronze_df.withColumn('churn',when(col('churn') == 'Yes',1).when(col('churn') == 'No',0).otherwise('Unknown'))\
                     .filter(col('contract') == 'Month-to-month')\
                     .filter(col('internetService') != 'No')
silver_df.show(5)

三. 卡普兰-迈耶生存曲线（Kaplan-Meier)

1
2
3
4
5
6
7
8
9
10
11
12
13
# 将Spark dataframe 转成 Pandas dataframe 便于对接第三方库lifelines
telco_pd = silver_df.toPandas()
telco_pd.head(5)

# 拟合Kaplan-Meier模型, 参数为Tenure和Churn
# 可视化生存概率曲线
kmf = KaplanMeierFitter()
 
T=telco_pd['tenure']
C=telco_pd['churn'].astype(float)
 
kmf.fit(T,C)
kmf.plot(title='Kaplan-Meier Survival Curve: Population level');

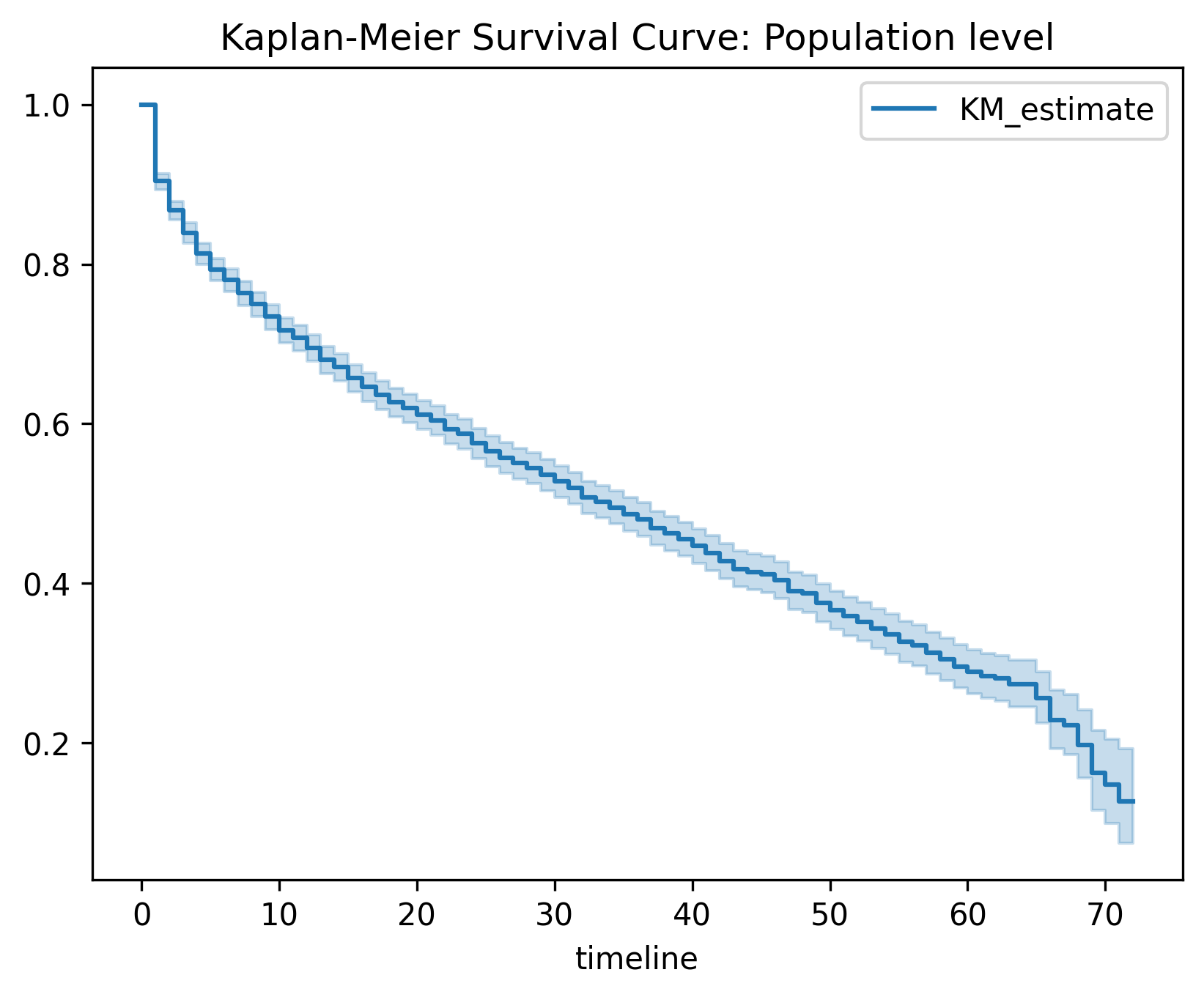
1. Kaplan-Meier曲线与协变量分组的理想情况

理想情况：不同组别的Kaplan-Meier曲线应表现出明显分离（如OnlineSecurity的”Yes”和”No”组），这表明该协变量对预测目标（如客户流失）有区分能力。

不理想情况：若曲线紧密重叠（如Gender的“Female”和“Male”组），则说明该变量可能对预测无帮助。

2. Log-Rank检验的作用

检验不同组别的生存曲线是否具有统计学差异。

原假设（H₀）：组间无差异。

备择假设（H₁）：组间存在差异。

若 p值 < 0.05，则拒绝H₀，认为组间差异显著（如OnlineSecurity）。

若 p值 ≥ 0.05，则无法拒绝H₀，认为组间可能无差异（如Gender）。

另外，test_statistic值越大差异越显著。

3. 利用Kaplan-Meier曲线预测与推断的不同视角

预测（Prediction）：目标是找到强相关特征以构建高精度模型。对于无差异的变量（如Gender）可以直接剔除，减少噪声。

推断（Inference）：目的是理解业务影响，即使变量无预测价值，也可能具有一定的决策意义（如免费提供某服务后，发现对用户留存无改善，决策者需要评估是否值得继续投入）。

4. 模型不适用的情况

Log-rank 检验假设各组风险比例恒定，若曲线交叉，需使用分段Log-Rank检验或Cox模型。

5. 模型结果与分析

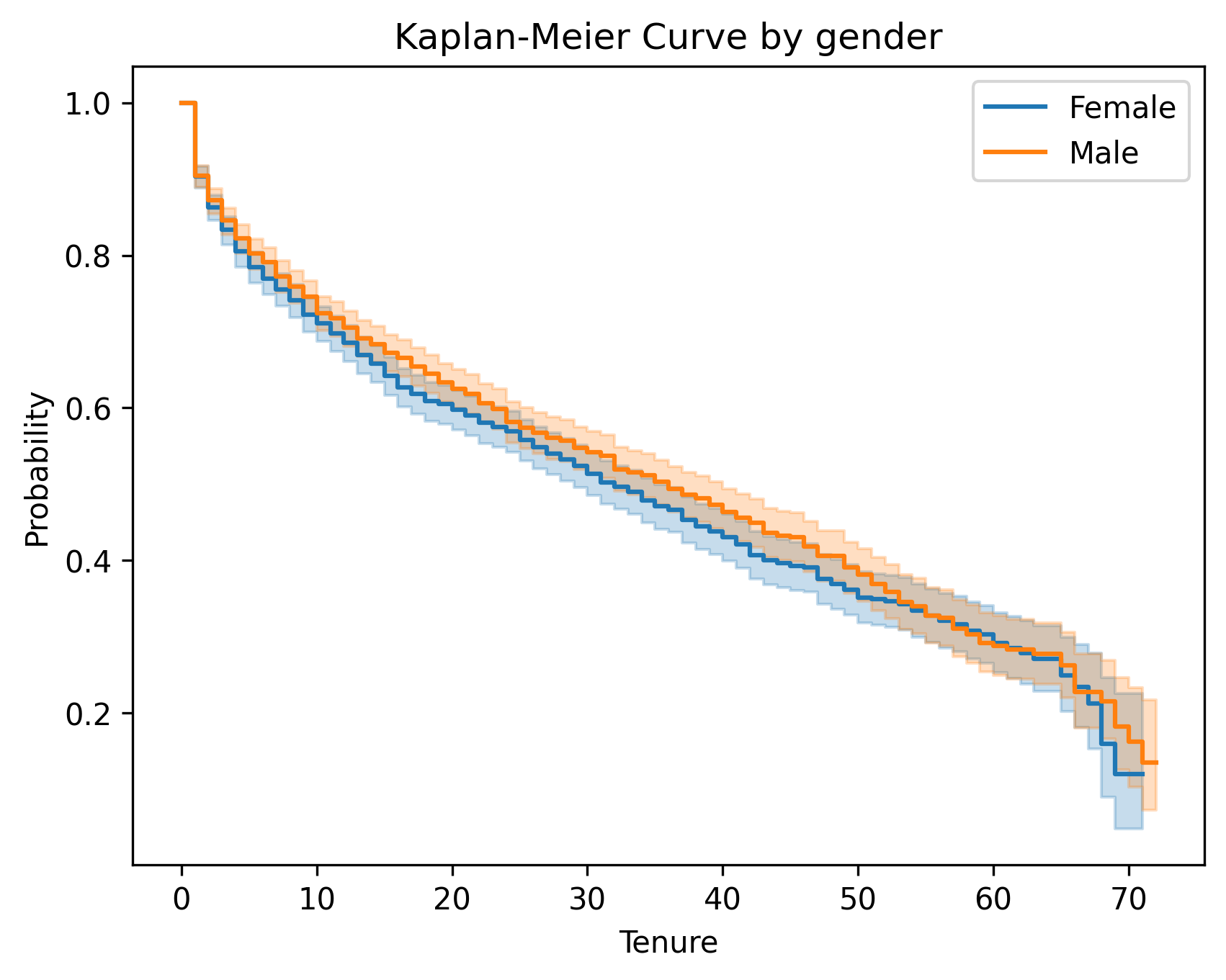
以下是按性别和是否开启网络安全服务变量画出的Kaplan-Meier曲线和Log-Rank检验

  • OnlineSecurity就是一个很好的例子, 他的生存曲线能明显分离，进一步Log-Rank检验的p值非常小，我们能判断组间差异明显。
  • 相反，Gender的生存曲线非常接近，那就不太理想。当生存曲线非常接近时，我们需要进一步进行 Log-Rank 检验。以判断组之间在统计上是否等价。结果我们对于性别的 Log-Rank 检验的 p 值大于 0.05，因此我们无法拒绝两个组在统计上等价的原假设。
variable test_statistic p -log2(p)
Female / Male 1.61011 0.204476 2.289995
variable test_statistic p -log2(p)
No / Yes 75.800079 3.138886e-18 58.144453

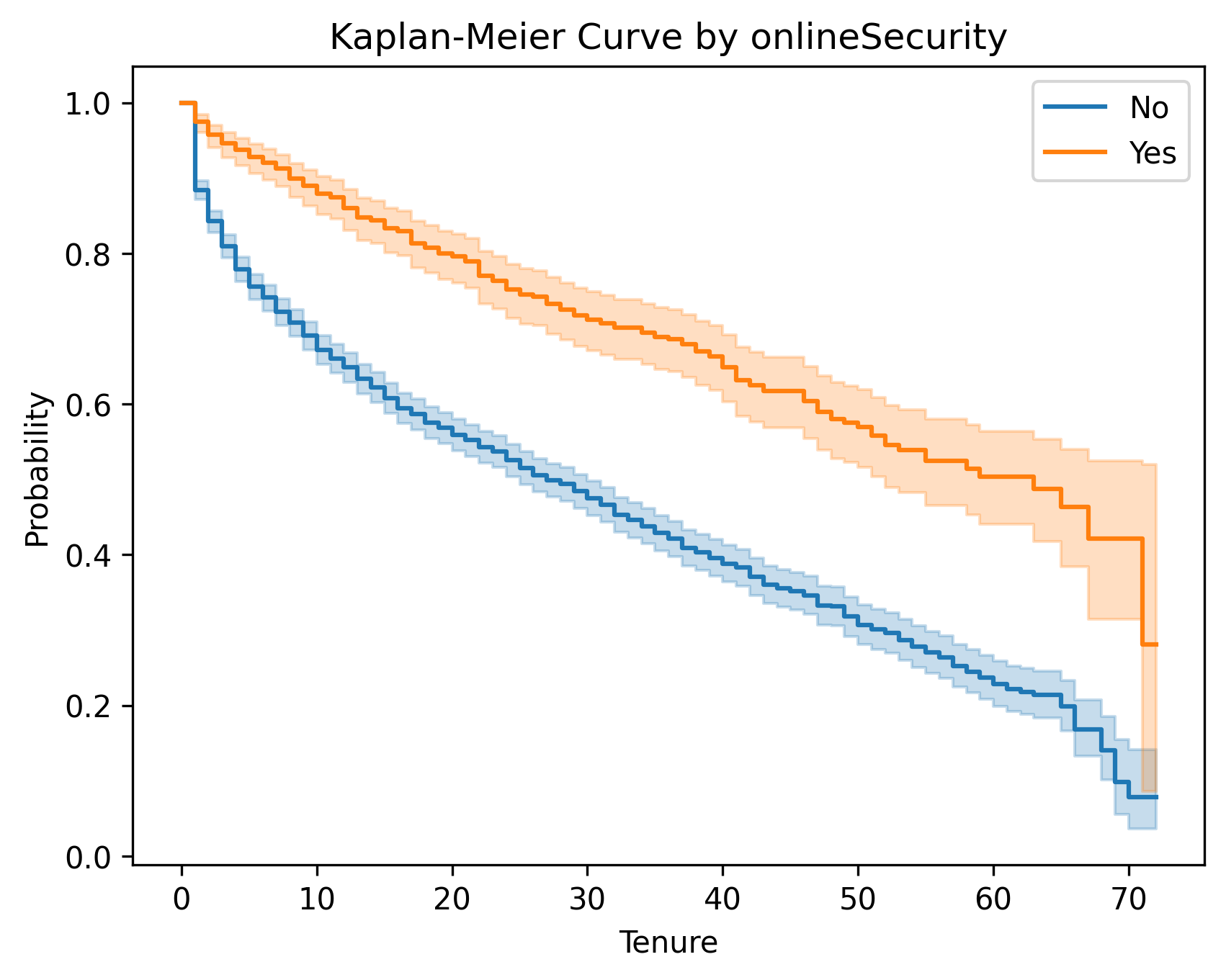
以下表格记录了Kaplan-Meier法的结果

变量 Kaplan-Meier曲线 Log-rank检验p值
Gender 基本重合 p = 0.20
seniorCitizen 略微分离 p < 0.05
partner 明显分离 p < 0.05
dependents 明显分离 p < 0.05
phoneService 略微分离 p = 0.38
multipleLines 明显分离 所有p值均小于0.05
internetService 明显分离 p < 0.05
onlineSecurity 明显分离 p < 0.05
onlineBackup 明显分离 p < 0.05
deviceProtection 明显分离 p < 0.05
techSupport 明显分离 p < 0.05
streamingTV 略微分离 p < 0.05
streamingMovies 略微分离 p < 0.05
paperlessBilling 明显分离 p < 0.05
paymentMethod 除Bank transfer和Credit card曲线基本重合
其他曲线明显分离		 除Bank transfer和Credit Card的p = 0.70
其余p < 0.05

  • 其中性别对流失无影响，无需针对性营销 。

  • 使用银行转账或信用卡支付的客户，其流失风险在统计学上无法区分。

四. Cox比例风险模型(Cox Proportional Hazards)

1. Cox比例风险模型 vs Kaplan-Meier方法

维度 Kaplan-Meier Cox比例风险模型
功能 估计生存概率 $S(t)$ 估计风险比
输入 单变量分组 多变量联合分析
输出 生存曲线 风险比 $\exp(\beta)$ 和 p值

风险（Hazard） 是生存的“反面”。

2. Cox模型核心公式

$$h(t \mid X) = h_0(t) \cdot \exp(\beta_1 X_1 + \dots + \beta_p X_p)$$

其中，基线风险 $h_0(t)$ 所有协变量取基准值时的风险函数；部分风险 $\exp(\beta X)$表示协变量偏离基线值时对风险的影响。

3. 比例风险假设

  • 不同组别之间的风险比随时间保持恒定。

  • 因为基线风险仅与时间$t$相关，描述所有协变量取基准值时风险随时间的变化模式。

  • 部分风险仅与协变量$X$相关，表示协变量对风险的乘性影响，且不随时间变化。

4. 如何验证假设

  • 方法 1: 统计学检验: p值小于0.05代表违反了假设。

    1
    cph.check_assumptions(df,p_value_threshold=0.05)

  • 方法 2: Schoenfield残差：通过残差与时间的关系图，直观判断变量风险比是否随时间变化, 残差与时间有任何趋势代表违反假设。

    1
    cph.check_assumptions(..., show_plots=True)

  • 方法 3: Log-log Kaplan-Meier曲线：绘制不同组的 $ \log(-\log(S(t))) $ 曲线，若曲线平行则假设成立。

5. 假设违反的解决方案

（1）保持原模型

  • 适用于预测场景而非因果推断。
  • 在这种情况下关注模型在测试集上表现良好（如Concordance指数高）。

（2）使用分层模型（Stratified Cox Model）

  • 原理：对违反假设的变量分层，每组独立估计基线风险 $ h_0(t) $，共享其他变量系数。

  • Python示例: 

  • cph.fit(df, strata=['onlineBackup_Yes'], duration_col='tenure', event_col='churn')

    1
    2
    3
    4
    5
    6
    7
    8
    9

    **（3）引入时变协变量（Extended Cox Model）**

    - **原理**：通过交互项捕捉风险比随时间的变化

    - **Python示例**：

    - ```python
      df['backup_time'] = df['onlineBackup_Yes'] * df['tenure']  # 创建时间交互项

  • 适用场景：已知风险比随时间线性变化。

（4）使用样条函数或分段常数风险

  • 原理：将时间轴分段，每段内基线风险为常数或平滑曲线。

  • 优势：可以灵活拟合复杂的时间模式。

  • Python示例： 

    1
    2
    from lifelines import PiecewiseExponentialFitter
    pwf = PiecewiseExponentialFitter(breakpoints=[0, 6, 12]).fit(df, 'tenure', 'churn')

（5）改用别的模型（如加速失效时间模型AFT）

  • AFT模型：假设生存时间 ( T ) 服从特定分布（如Weibull、对数正态），直接建模生存时间而非风险函数。
  • 适用场景：
    • PH假设严重违反且无法修正。
    • 生存时间有明显参数分布特征。

6. 模型评估

1. 协变量统计显著性检验

  • 判断标准：
    • p值 < 0.05 → 统计显著
    • p值 ≥ 0.05 → 考虑删除或调整

2. 系数估计的置信度

  • 评估方法：
    • 检查exp(coef)的95%置信区间
    • 若区间包含1($e^{0}$),可认为该变量不显著

3.示例

  • internetService_DSL的exp(coef) = 0.80，说明使用DSL的客户流失风险是基准组的 80%（风险降低20%）。

4.模型比较指标

指标名称 解释
Concordance 模型预测的正确排序概率，表示区分能力，越接近1说明区分能力越强
Partial AIC 考虑拟合优度和复杂度的信息准则，值越小模型越好
Log-likelihood Ratio Test 对数似然比，检验模型是否优于空模型，$p<0.05$ 或者 $χ^2 > χ_{0.95/0.99}^2(自由度)$说明显著改进

7. 模型结果与分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 将五列分类变量进行独热编码
encode_cols = ['dependents','internetService','onlineBackup','techSupport','paperlessBilling']
 
encoded_pd = pd.get_dummies(telco_pd,
               columns=encode_cols,
               prefix=encode_cols,
               drop_first=False)
# 创建一个新dataframe，仅包含拟合模型所需的变量
survival_pd = encoded_pd[['churn','tenure','dependents_Yes','internetService_DSL','onlineBackup_Yes','techSupport_Yes']]
# churn列转换为float类型
survival_pd.loc[:,'churn'] = survival_pd.loc[:,'churn'].astype('float')

# 我们将使用 95% 的置信区间进行统计检验。
# 打印模型拟合的结果
cph = CoxPHFitter(alpha=0.05)
cph.fit(survival_pd, 'tenure', 'churn')
cph.print_summary()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
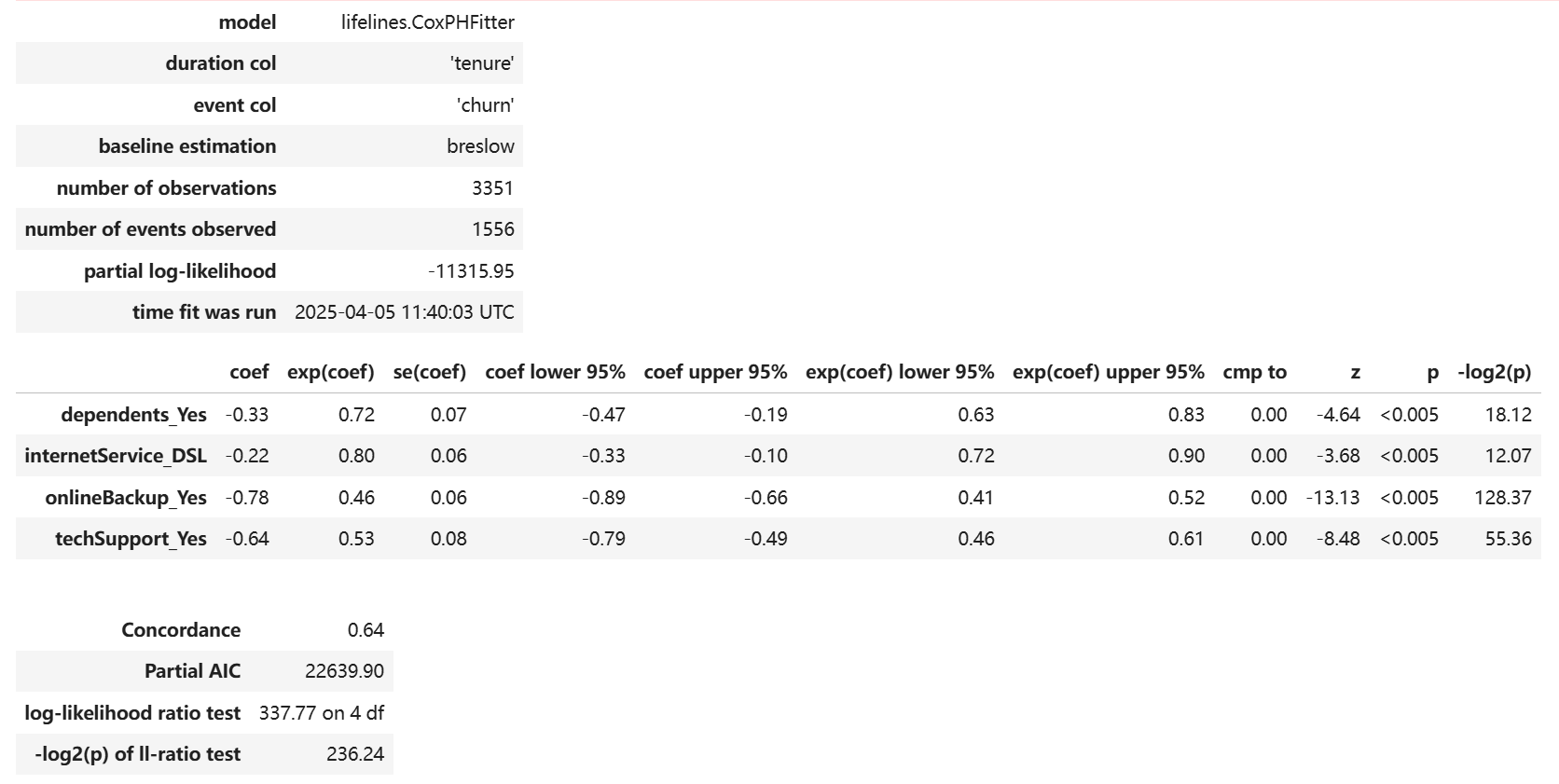
# 检验是否违反假设，方法1,2
cph.check_assumptions(survival_pd,p_value_threshold=0.05,show_plots=True)

# 检验是否违反假设，方法3
# 拟合Kaplan-Meier模型
kmf = KaplanMeierFitter()
 
T=telco_pd['tenure'] 
C=telco_pd['churn'].astype(float)
 
kmf.fit(T,C)

# 绘制log-log Kaplan-Meier曲线
def plot_km_loglog(col):
  ax = plt.subplot(111)
  for r in telco_pd[col].unique():
    ix = telco_pd[col] == r
    kmf.fit(T[ix], C[ix],label=r)
    kmf.plot_loglogs(ax=ax)

由以上三个检验可知, techSupport, internetService, dependents 三个变量都违反了比例风险假设。

五. 加速失效时间模型(Accelerated Failure Time)

1. 核心概念

  • AFT模型是一种参数模型，假设生存时间 ( $T$ ) 服从特定的布（如Weibull、对数正态等）。其核心思想是：不同组别的生存时间存在”加速”或”减速”效应。

  • 参数模型通常比非参数和半参数模型的“灵活性”较低，但当你对指定结果变量的分布感到满意时，它可以是一个不错的选择。

  • 例子：

    • 狗的寿命 ≈ 人类寿命 × $ \frac{1}{7} $
    • 即狗的生存时间被”加速”了7倍（经历相同生命阶段但更快）。

2. 与Cox/KM模型的对比

特性 AFT模型 Kaplan-Meier Cox模型
模型类型 参数化 非参数化 半参数化
分布假设 需指定T的分布 无分布假设 无基线风险分布假设
灵活性 最低 最高 中等
输出解释 时间加速因子 生存概率 风险比(HR)

3. 数学模型

核心方程：
$$
S_A(T) = S_B(t) \times \lambda
$$

  • $S_A(T)$: A组的生存函数
  • $S_B(T)$: B组的生存函数
  • $\lambda$: 加速失效率

对数Logistic分布示例：
生存函数：
$$
S(t) = \frac{1}{1 + (\lambda t)^p}
$$

4. 关键假设

  1. 比例时间假设：加速因子λ不随时间变化
  2. 分布假设：生存时间T服从指定分布（需验证）

5. 如何验证假设

AFT模型需要验证两个关键假设：

  1. 比例几率假设 → 要求log-log图曲线平行
  2. 分布适配性假设 → 要求log-log图曲线呈直线

验证方法: 以 $ \log(t) $为X轴，$ y $ 为Y轴绘图

Log-Logistic分布的Y轴公式 ：$y = \log\left(\frac{1 - S(t)}{S(t)}\right)$

6. 假设违反的解决方案

(1) 尝试其他分布

(2) 使用半参数模型

(3) 分层分析

7. 模型评估

1. 协变量统计显著性检验

  • 判断标准：
    • p值 < 0.05 → 统计显著
    • p值 ≥ 0.05 → 考虑删除或调整

2. 系数估计的置信度

  • 评估方法：
    • 检查exp(coef)的95%置信区间
    • 若区间包含1,可认为该变量不显著

3. 示例

  • internetService_DSL的exp(coef) = 1.47，说明当客户使用Fiber Optic服务时，他们的流失时间加速了 1.47 倍。

4. 模型比较指标

指标名称 解释
Concordance 模型预测的正确排序概率，表示区分能力，越接近1说明区分能力越强
AIC 考虑拟合优度和复杂度的信息准则，值越小模型越好
Log-likelihood Ratio Test 对数似然比，检验模型是否优于空模型，$p<0.05$ 或者 $χ^2 > χ_{0.95/0.99}^2(自由度)$说明显著改进

8.模型结果与评估

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 在这个例子中选取8个变量,并进行独热编码
encode_cols = ['partner','multipleLines','internetService','onlineSecurity', 'onlineBackup','deviceProtection','techSupport','paymentMethod']
 
encoded_pd = pd.get_dummies(telco_pd,
               columns=encode_cols,
               prefix=encode_cols,
               drop_first=False)

survival_pd = encoded_pd[['churn','tenure','partner_Yes', 'multipleLines_Yes', \
                          'internetService_DSL','onlineSecurity_Yes','onlineBackup_Yes','deviceProtection_Yes','techSupport_Yes',\
                          'paymentMethod_Bank transfer (automatic)','paymentMethod_Credit card (automatic)' ]]
# 在此notebook中假设生存时间T服从log-logistic分布,liflines还提供WeibullAFTFitter，LogNormalAFTFitter，LogLogisticAFTFitter，ExponentialAFTFitteraft.print_summary()
aft = LogLogisticAFTFitter()
aft.fit(survival_pd, duration_col='tenure', event_col='churn')
aft.print_summary()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
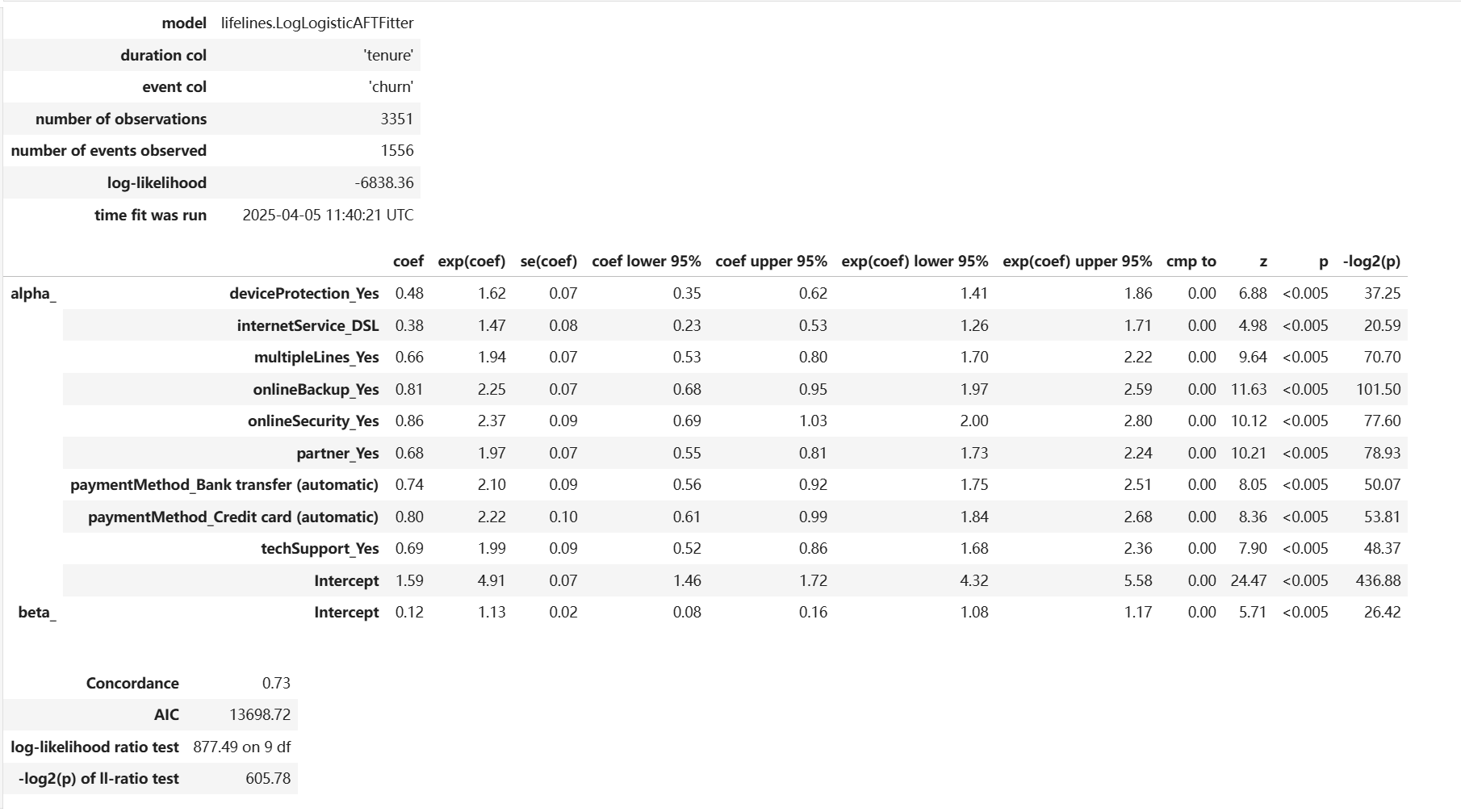
# 拟合KaplanMeier模型便于检验假设是否成立
from lifelines import KaplanMeierFitter
kmf = KaplanMeierFitter()
 
T=telco_pd['tenure'] #duration
C=telco_pd['churn'].astype(float) #event observed
 
kmf.fit(T,C)

# 以log(1-sf)/sf为y轴，log(t)为x轴画图
def plot_km_logOdds(col):
  ax = plt.subplot(111)
  for r in telco_pd[col].unique():
    ix = telco_pd[col] == r
    kmf.fit(T[ix], C[ix],label=r)
    sf = kmf.survival_function_
    sf['failureOdds'] = (np.log(1-sf))/sf
    sf['logTime'] = np.log(sf.index)
    plt.plot(sf['logTime'],sf['failureOdds'])
  • 总体而言，每个图中的线条相对直。这有一些偏差，但整体上并不严重。这表明选择log-logistic 作为指定分布是一个合理的选择。
  • 总体而言，每个图中的线条并不平行。这表明加速失效时间模型不适用于指定的模型。

六. 利用Cox比例风险模型进行可视化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
# 选出其中的五列，进行独热编码
# 拟合出Cox比例风险模型
# 此步与第五部分相同
encode_cols = ['dependents','internetService','onlineBackup','techSupport']
 
encoded_pd = pd.get_dummies(telco_pd,
               columns=encode_cols,
               prefix=encode_cols,
               drop_first=False)
 
survival_pd = encoded_pd[['churn','tenure','dependents_Yes','internetService_DSL','onlineBackup_Yes','techSupport_Yes']]
survival_pd.loc[:,'churn'] = survival_pd.loc[:,'churn'].astype('float')
cph = CoxPHFitter(alpha=0.05)
cph.fit(survival_pd, 'tenure', 'churn')
# 创建控件
cols = ['dependents_Yes', 'internetService_DSL', 'onlineBackup_Yes', 
        'techSupport_Yes', 'internal_rate_of_return']

widget_dict = {
    col: widgets.Dropdown(options=[('No', 0), ('Yes', 1)], value=0, description=col)
    if col != 'internal_rate_of_return' 
    else widgets.FloatSlider(min=0.00, max=0.5, step=0.01, value=0.10, description='IRR')
    for col in cols
}

# 定义计算函数
def calculate_payback(dependents_Yes, internetService_DSL, onlineBackup_Yes,
                     techSupport_Yes, internal_rate_of_return):
    
    # 构建输入DataFrame
    input_data = pd.DataFrame({
        'dependents_Yes': [dependents_Yes],
        'internetService_DSL': [internetService_DSL],
        'onlineBackup_Yes': [onlineBackup_Yes],
        'techSupport_Yes': [techSupport_Yes],
        'internal_rate_of_return':[internal_rate_of_return]
    })
    # 计算生存概率 
    survival_probs = cph.predict_survival_function(input_data)
    survival_probs = pd.concat([
        pd.Series([1.0], index=[0]),  # 添加初始点
        survival_probs 
    ])

    # 计算结果DataFrame
    irr_monthly = internal_rate_of_return / 12
    months = survival_probs.index
    monthly_profit = 30  # 假设每月利润为30, 需要按具体情况调整
    
    result_df = pd.DataFrame({
        'Contract Month': months + 1,
        'Survival Probability': survival_probs[0].round(2),
        'Monthly Profit': monthly_profit,
        'Expected Profit': (survival_probs[0] * monthly_profit).round(2),
        'NPV of Profit': (survival_probs[0] * monthly_profit / (1 + irr_monthly)**months).round(2)
    })
    result_df['Cumulative NPV'] = result_df['NPV of Profit'].cumsum()
    
    #可视化
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
    
    # 生存曲线
    ax1.plot(result_df['Contract Month'], result_df['Survival Probability'], 
            marker='o', color='b')
    ax1.set_title('Survival Probability Over Time')
    ax1.set_xlabel('Contract Month')
    ax1.set_ylabel('Survival Probability')
    ax1.grid(True)
    
    # 累计NPV
    ax2.plot(result_df['Contract Month'], result_df['Cumulative NPV'], 
            marker='s', color='r')
    ax2.set_title('Cumulative NPV of Customer')
    ax2.set_xlabel('Contract Month')
    ax2.set_ylabel('Cumulative NPV ($)')
    ax2.grid(True)
    
    plt.tight_layout()
    plt.show()
    
    # 返回表格数据
    display(result_df.set_index('Contract Month'))
1
2
3
4
5
6
7
8
9
# 创建交互界面
interact(
    calculate_payback,
    dependents_Yes=widget_dict['dependents_Yes'],
    internetService_DSL=widget_dict['internetService_DSL'],
    onlineBackup_Yes=widget_dict['onlineBackup_Yes'],
    techSupport_Yes=widget_dict['techSupport_Yes'],
    internal_rate_of_return=widget_dict['internal_rate_of_return']
);

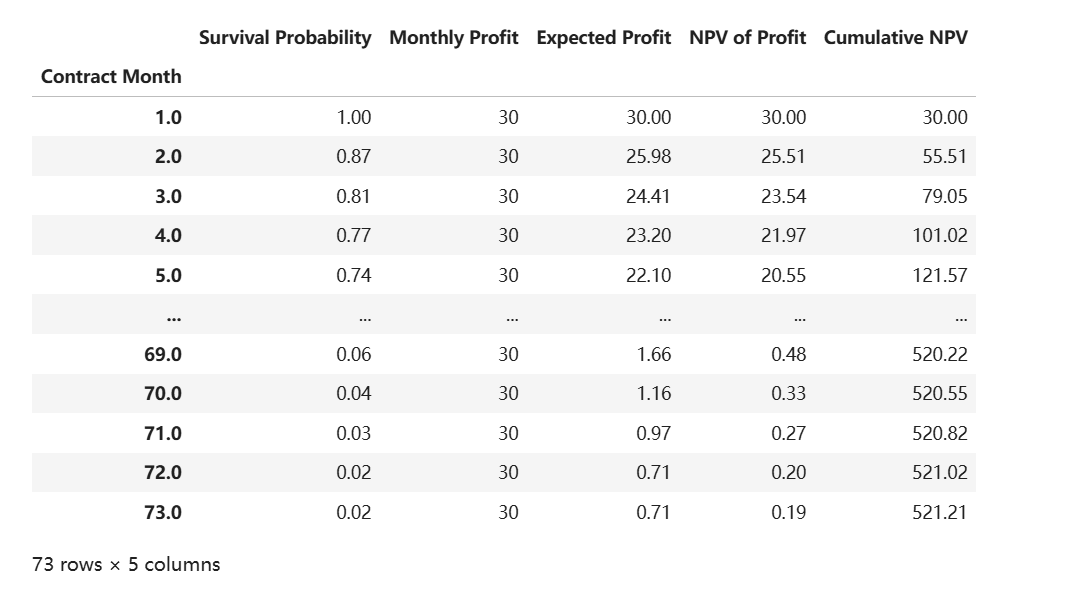
可视化生存曲线与收益曲线

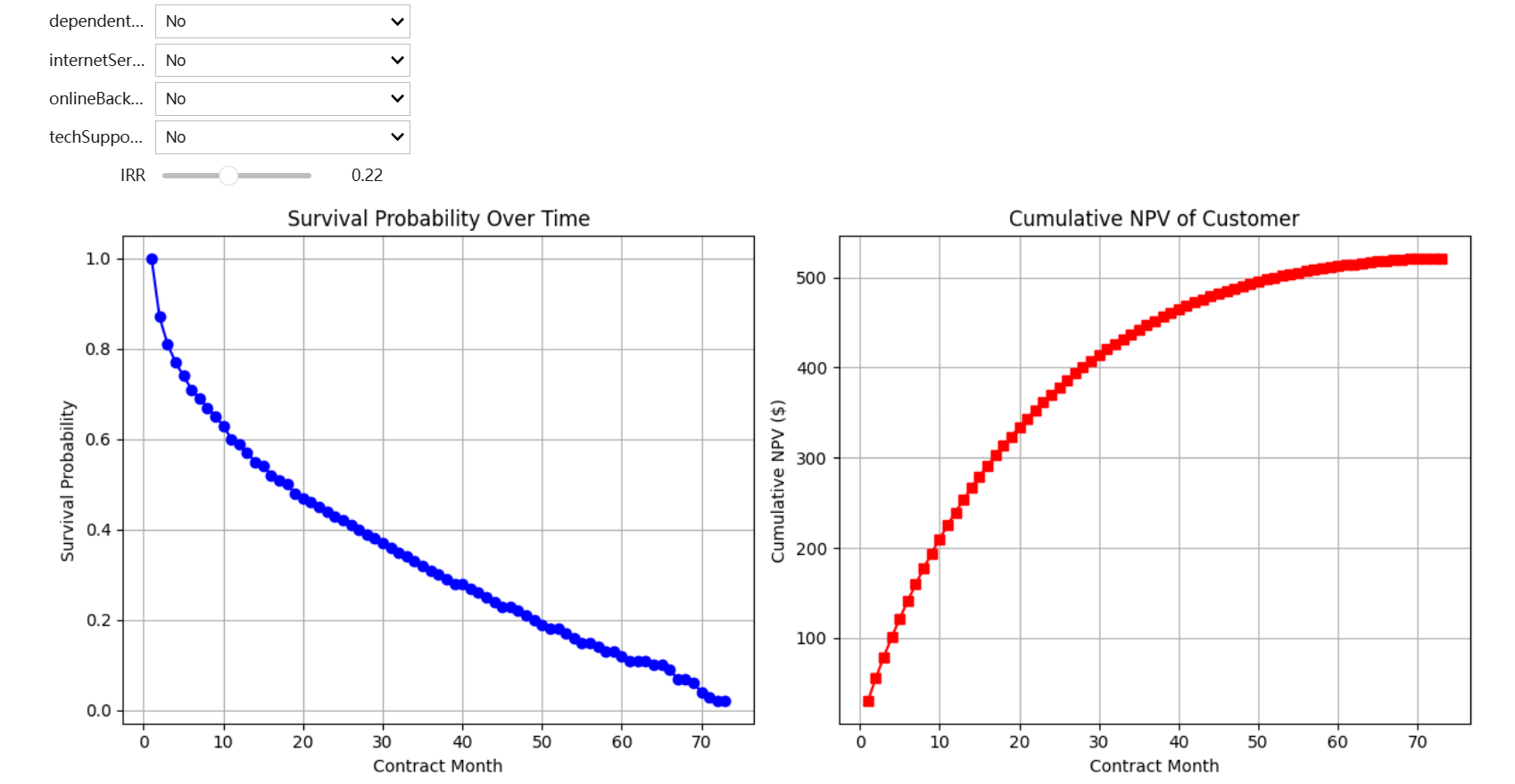
可视化客户生命周期价值分析表

名称
 说明 计算公式
合同月份
(Contract Month)		 客户签约后的月份序号 -
生存概率
(Survival Probability)		 客户在当月的留存概率，来自Cox比例风险模型预测 predict_survival_function()
月利润
(Monthly Profit)		 该服务方案的月利润
（当前设定为30，实际需替换为业务数据）		 -
月均预期利润
(Avg Expected Profit)		 考虑留存率后的实际月利润期望值 生存概率 × 月利润
利润净现值
(NPV of Profit)		 基于时间价值的利润折现
（默认内部收益率10%，需按业务调整）		 月均预期利润 / (1 + 月化内部收益率)^合同月份
累计净现值
(Cumulative NPV)		 客户累计产生的总价值 各月利润净现值的累加和